Using Personal Math Instead Of Abstract Theory To Make Better Retirement Decisions
By Daniel R. Amerman, CFA
TweetWhen it comes to financial analysis, the person who controls the assumptions can also be the person who controls the results. So, if someone is relying on the advice of an authority to help them make an important personal financial decision - they are also necessarily relying on that person's assumptions.
This can create a potential problem if the person who is making the important personal decision doesn't agree with the assumptions used by the authority. There is the danger of someone making key lifetime decisions based upon assumptions that they would emphatically disagree with - if only they fully understood those assumptions.
A recent study by the Stanford Center On Longevity concluded that for middle-income retirees, Social Security was likely to account for between 50% and 85% of their total retirement income.
Because a typical retirement can last for 15 to 20 years or more, and the money provided by Social Security is likely to be the largest source of income during those years - choosing at what age to claim Social Security can be one of the single most important financial decisions that an average person will make in their lifetime.
Based on some simplifying assumptions, academic researchers have generally concluded that there is a strong incentive for most people to defer claiming Social Security benefits, with waiting until age 70 being common advice. These analyses have been widely publicized in the financial media, and have become what is treated as the conventional wisdom.
The consensus seems impressive - but, what if those results were completely dependent upon assumptions that many or most people would disagree with? What if we run the same analysis, but with assumptions that you do agree with, and we come up with quite different results? Would that lead to better retirement decisions - for you?
This analysis is a dissent from the conventional wisdom, and it is based on a quite different starting assumption - that when it comes to one of the most important financial decisions that a person will make, we should individually get to choose our own assumptions. It is part of a series of related analyses, an overview of the rest of the series is linked here.
The Basic Equations For Making Social Security & Retirement Choices
When it comes to making essential financial decisions for retirement we need to carefully consider the relationship between time and money.
For decisions such as when to begin collecting Social Security, we are looking at different amounts of money at different points in time. We get less money per month if we claim early - such as at age 62 - but we do get it for a longer period of time, We get more money per month down the road if we claim late - such as at age 70 - but the price is that we have to give up all of our cash flows before that time.
We could just add up the monthly payments with each option and compare them (which some simplistic models do).
However, the issue is that inflation means that the farther out in time we go - the less a dollar is worth. We will make better decisions if we take the changing value of money over time into account. More sophisticated analyses use "purchasing power" to do this, where the value of each future cash flow is adjusted using an assumed rate of inflation. This allows us to make "apples to apples" comparisons where all cash, whenever received, is brought to the common terms of what it would buy today.
The two core equations which are used for this type of analysis are the future value equation and the present value equation. In the next sections we will take a very quick and simple look at those formulas, and how they are used for making retirement decisions.
Looking at the actual formulas is somewhat unusual in an analysis that is intended for a general audience - but it is an essential step. The reason is that in the process of doing so, we can get to some critically important theoretical simplifying assumptions that the conventional wisdom is based upon. This will allow you to decide for yourself whether you believe them or not, and whether you should make one of the most important financial decisions of your life based upon those assumptions.
Future Value & Sending Cash Forward Through Time

The future value equation is shown above. We have FV, which is future value, and that's going to be the actual cash flow received in period "n", with no adjustment for inflation. The way we calculate it is we take our starting cash flow - cash flow in year zero - and we multiply it times one plus "i", raised to the nth power, where "n" equals the number of years into the future that we are looking.
The variable "i" can be any one of a number of different things. For example, it could be an interest rate, and if so, then our future value equation above becomes the classic compound interest equation.
An equation of this sort is also essential when making better retirement decisions. Social Security is indexed for inflation, it is a COLA based retirement cash flow. Social Security is in theory supposed to fully keep up with inflation, with the benefits increasing each year at exactly the rate of inflation. So the variable "i" is now defined as the rate of inflation, and our future cash flow increases in each year, by an amount that depends on the rate of inflation.
As an example let's say that inflation is 3% every year, our Social Security benefit also goes up by exactly 3% each year, and we want to calculate how much cash we will be getting 10 years from now.

Let's start with a round number $1,000 monthly benefit. We add our 3% rate of inflation to the number one, getting 1.03, and we raise that to the 10th power. We take that number and multiply it times our starting cash flow.
What this tells us if we have a $1,000 monthly Social Security benefit and we get 10 years of 3% annual increases which exactly equal the 3% rate of inflation, we will be getting $1,344 a month in ten years.
Present Value & Bringing Cash Back In Time: The One Factor Approach
Now the issue is that the reason our benefit is going up is because inflation is reducing the value of the dollar. So it's not like we really have the equivalent of $1,344 dollars in purchasing power today, but rather we have more dollars to offset the effects of each dollar buying less.

The other core equation that we use when we're looking at the value of cash flows at different points in time is what is known as the present value equation. At its core, present value (PV) is equal to future value, discounted back in time. If we take the future value - the dollars we will receive in the future - and divide it by 1 + "i" raised to the "n", then we get the value today, which is the present value.

Another way of looking at this is that since we know the equation for future value, we can substitute that equation for FV into our present value equation. So, if we express that in a little bit different way, what we have is that present value equals starting cash flow times one + "i", raised to the "n", and then divided by one + "i", also raised to the "n". Now, that's a very interesting equation.

Simple algebra tells us that we can cancel out "1 + i raised to the n" on both the top and bottom of our fraction, the numerator and the denominator.
Rephrased, so long as we have a one factor model for inflation, where there is a single rate equal to "i", and "i" therefore equals "i" on both top and bottom, then we can cancel out and we're left with the equation below.

The real value, the present value, of every cash flow in the future is equal to the beginning cash flow at time zero. From the perspective of theoretical finance - this is a very useful simplification.
Because "i" has canceled out, the rate of inflation no longer matters. Because "n" has cancelled out, it doesn't matter how many years in the future we go. Whatever the rate of inflation or whatever the year, the present value of each future cash flow is equal to its starting amount.
What is being shown here is perfect inflation indexing. It is based upon the core simplifying assumption that annual Social Security benefit increases will with 100% certainty always exactly match the real rate of inflation that is being experienced by the person making the retirement decision.

A present value numerical example is shown above, which corresponds to the earlier future value example. We could go to the trouble of figuring out what 1.03 raised to 10th is, and multiply and then divide by it, but why bother? The payment is worth $1,000 in year 10 - and year 5, and year 20 and even year 30 or year 40. It also doesn't matter whether the rate of inflation is 1%, 5% or 10% - with the perfect inflation indexing that is created by using only one inflation factor, the present value of the future value is always equal to $1,000.
Now many people are not aware of this, but it is a core underlying assumption for the great majority of the financial models used to make Social Security claiming decisions.
It also should be noted that this assumption of perfect inflation indexing leads us to somewhere that is very unusual for those with training in finance, economics or accounting. Once we cancel out top and bottom, and "n" disappears from the equation - the time value of money has also disappeared. It no longer matters when we get our money - it is always worth the same. So a payment received at age 62 is worth the same as a payment at age 72, and a payment at age 82 and a payment at age 92.
With no effective time value for money, then payments that are assumed to be received in 15 years or 30 years can be treated as being every bit as valuable today as a payment that we would get next month. Indeed, it is those very high values for payments that we assume will be received with perfect reliability in the distant future, that are responsible for the model results that lead to the widespread advice to defer claiming Social Security.
It should also be noted that there are different approaches that can be taken, other equations that can be used instead of the very simple ones used above. However the key assumptions are those of 1) perfect payment reliability; and 2) perfect inflation indexing.
1) Perfect Payment Reliability. Every payment will be received in full under the current Social Security regulations, with no modifications or reductions whatsoever, and this will remain true no matter how many years we look into the future.
2) Perfect Inflation Indexing. The annual benefit increases will always exactly equal the rate of inflation and will increase the cash flow in such a way that purchasing power is perfectly maintained, no matter how far in the future we go, or what rates of inflation are experienced in practice.
So long as those assumptions both hold true - then this special case of the disappearance of the time value of money can work, and any number of experts using those same assumptions can agree that the most financially advantageous strategy is to wait to claim the Social Security benefits.
However, if those theoretical assumptions do not hold true - if you do not agree with their applicability in your life and in the real world - then we are left with a quite fragile and theoretical mathematical special case, which is subject to collapse in the real world.
Using Two Inflation Factors Instead Of One
For the next step in this analysis we are going to commit a radical act of common sense. We are going to use a two factor model for inflation, with two different values for "i".

For our future value equation, in the top half of the fraction we will replace "i" with "gi". What "gi" represents is a real world number, which is the actual rate at which the government increases Social Security benefits payments.
Over the last three years, these annual increases have averaged about 0.75%.
In the bottom half of the fraction where we discount to bring our future value back to its value in the present, we will use "pi" instead of "i". What "pi" represents is not the famous irrational number, but rather our best personal estimate for the rate of inflation.
After all - the experts agree that the practical application of these financial equations are what should guide one of the single most important financial decisions that an average person will make in their lifetimes. Shouldn't an individual have some input on what assumptions will be used for making a decision that could be the primary determinant of his or her personal standard of living for decades?
As an example, let's return to the last three years. An individual may not believe that a 0.75% rate of inflation has been applicable for their own life. They disagree that the rate at which the government has been raising Social Security benefits accurately corresponds with what they have been paying for their purchases. Perhaps they believe that a 2.0% rate of inflation (as an example) would be a much more accurate number, when it comes to what has been happening to the purchasing power of their own money.
So, let's run our new equation with gi, Social Security benefit increases, equalling 0.75%, and pi, our personal best estimate for inflation in our own life equaling 2.0%.
The first thing that happens is that we have a complete collapse of the one factor inflation model.

With a different "i" on top and bottom, we can't cancel out anymore, and our neat little mathematical simplification trick is no longer valid.
Instead we have two exponential series that will be diverging and how far they diverge changes with any change in rate or any change in time. The equation now becomes acutely sensitive to the difference between "gi" and "pi" and the results will be different at every time point in the future.

Let's return to our valuation for what a Social Security payment in ten years is worth to us today. We send the money forward in time with our future value equation on top, and a compounding rate that is equal to "gi", which is 0.75% per year. We bring the money back in time with the discounting component of our present value equation on bottom, and a compounding rate that is equal to "pi", which is 2.0% per year.
When we do the math, the result is that $1,000 is no longer $1,000. Instead, if our benefits are only going up by 0.75% per year, and the rate of inflation we experience is equal to 2.0% per year, then the purchasing power of the monthly payment in ten years is only $884.
The payment has lost 11.6% of its value. If we look at this on an annual basis, then what was 365 days of purchasing power has become 323 days of purchasing power. If we needed every bit of our annual payments to meet our expenses, then in ten years we would have 46 weeks of purchasing power to cover 52 weeks of expenses, leaving us 6 weeks short.
In order to make the best decision we can regarding what for most people will be one of the most important financial decisions of their lives - when to begin claiming their Social Security benefits - the key mathematical question is how we weight the value of near term cash flows versus medium term and long term cash flows.
When we reject the assumption of perfect inflation indexing and allow benefit increases to move at a different rate than the personal rate of inflation (either expected or experienced), then there is a fundamental change to the weighting of the value of the cash flows. This can mean that the best practical decisions for millions of retirees in the real world might be quite different than what academic theory would say.
Two Factors & Time

To see what a payment in 20 years is worth today, we need to change "n" from 10 to 20 on both the top and the bottom of the equation. We are now sending the money 20 exponential compounding periods into the future, and then bringing the money back 20 compounding periods to the present.
Remember, with perfect inflation indexing the value of that payment would be $1,000 today. However, when we use separate factors for benefit increases and personal inflation, then the value becomes only $781.
This is a decrease of 21.9% in purchasing power. For someone who needs 52 weeks of purchasing power to pay 52 weeks of expenses, they would be coming up 11 weeks short by the time they reach 20 years out.
The farther out we go in time - the greater the divergence between theoretical models that are based upon perfect inflation indexing, and real world results if things don't work out that way.
Now, let's consider a 62 year with good genes and in good health who fully expects to live into her 90s. She will need to cover a 30+ year period when comparing the value of cash flows in the present and in the future. With perfect inflation indexing and the one factor model, time becomes irrelevant, and the payment in 30 years is every bit as valuable as the one she might get next month.

However, when we go to the two factor model and we change "n" to 30 on both top and bottom, this means we are using 30 compounding periods, and the value of that payment in 30 years becomes worth only $691 today. This is a radically different outcome which can transform the retirement decision making process.
When we allow for two factors, and for inflation to move at a different and higher rate than actual Social Security benefit increases, then using the assumptions above, we get more than a 30% difference in valuation. So if there is only partial inflation indexing instead of perfect inflation indexing, then (with these assumptions) the theoretical simplification of assuming perfect indexing would be introducing a 30%+ model error for every single monthly payment received at age 92 and beyond.
When we correct for that error, the cash flows received in our 60s and 70s become substantially more valuable in relation to the cash flows received in our 80s and 90s - and the Social Security claiming decision can change.
Deeper Explorations
This topic is explored in much more detail in a (at this point) five part series on understanding the partial inflation indexing of Social Security, an overview of which is linked here.
The first analysis in that series (linked here) is enough by itself to disprove any assumptions of perfect inflation indexing. Benefits are paid on a monthly basis, but benefit adjustments are only made on an annual basis. The difference in frequencies and the difference between when measurements are made and when benefit increases are paid can be enough to materially reduce the present value of Social Security payments even if we keep the assumption that benefit increases exactly equal the annual rate of inflation.

This may sound trivial, but the real world impact can be quite significant when we use a more mathematically accurate formula for calculating the present value of Social Security payments, and this is particularly true at higher rates of inflation, as shown in the table above.
The second and third analyses in the series explore in much more detail the implications of having a rate of inflation that is even slightly different from the rate of growth in benefit increases, and what the real world implications for retirees can be on a year by year basis.
Those analyses also look at the many real world reasons to believe that benefit increases will not be equal to the personal rates of inflation that will be experienced by many or most retirees.
As an example, something that receives too little attention is that Social Security benefit increases are based upon an obscure inflation index called the CPI-W. The CPI-W is an index that measures only the expenses of urban workers. Which means that by definition - the expenses of retirees are entirely excluded, because they aren't currently working.
This creates a stark contrast between abstract theory and practical reality. Perfect inflation indexing is a very powerful simplifying assumption, that might seem reasonable. But in practice (and quite ironically), actual Social Security benefit increases are determined by using an inflation index that by design does not take into account retirees, their often different spending patterns, and what can be their different average rates of inflation.
The Critical Intersection Between Social Security & Medicare Premiums
There is one group that is likely to be particularly skeptical about the theory of perfect inflation indexing. That would be people who are currently retired, and are participating in both Social Security and Medicare.
As covered in the Part 4 analysis, the average Social Security monthly benefit has increased by $31 over the last three years. During that same time, base Medicare Part B premium deductions have gone up by $29 per month. So the net monthly benefit being received by the average retiree has gone up by only $2 over a period of three years.
There is a stark contrast between theory and what is happening right now in the real world. On the one hand, we have the experts agreeing to their equations and simplifying assumptions, whereby the perfect inflation indexing of Social Security can be mathematically proven to reliably create financial miracles for people in the distant future, if only they will be patient and not take the cash too soon.
On the other hand, in the messy reality of the present, we have a train wreck in progress with the effective inflation indexing of net Social Security benefits. As explored in the Part 4 analysis, if we just use the CPI-U (not the CPI-W) as the accurate rate of inflation, and we extrapolate what has actually been experienced in the last three years into the future, then by 2022 the average retiree will have lost a full month out of the annual purchasing power for their Social Security benefits net of Medicare Part B, relative to 2015.
That is a potentially disastrous outcome for the standards of living and financial security of tens of millions of people. It is not at all what is supposed to happen. But yet, the conventional wisdom and the reported "best advice" don't seem to be changing in the slightest. There seems to be an almost complete disconnect between the mathematical serenity of the accepted theory, and what is actually being experienced by retirees in reality.
One could say that Medicare will be whatever Medicare is, and has nothing to do with Social Security, so it can be ignored when it comes to making optimal Social Security claiming decisions. Which is implicitly exactly what the conventional wisdom is based upon, with Medicare premiums being ignored.
Reality is (again) quite different as explored in the Part 5 analysis. The "hold harmless" provision of Social Security means that the age we claim Social Security can change the size of the Medicare premiums that we pay. If Medicare premiums increase substantially in a year, then some retirees who are claiming Social Security can have the ability to effectively send at least a portion of their premium increases to other retirees who are in Medicare but are not yet claiming Social Security, and say "pay this for me."
There is also the issue that the whole purpose of delaying Social Security is to get larger benefits instead of smaller benefits. However, as explored in the Part 5 analysis, how "hold harmless" works is that people with smaller benefits can sometimes pass part of their Medicare premium increases on to the people with larger benefits. So, there is a potential dual financial modification to the cash flows that is being completely ignored in the conventional models, because of the simplifying assumption that ignores the financial interrelationship between Social Security benefits and Medicare premiums for retirees.
Assuming Promises Into Existence With Perfect Certainty
Some people might say that because the United States government has promised to make Social Security benefit payments in full into the distant future and to fully inflation index those payments, that it is indeed appropriate to treat both the payments and the indexing as being risk free. Valuing the cash flows from Social Security could be viewed as similar to valuing long term Treasury bond cash flows.
There is a really big problem with that reasonable sounding perspective, however - it isn't even remotely true. Yes, the government has promised to make principal and interest payments in full on long term Treasury bonds. But the federal government has not promised to make Social Security payments in full, or to increase those payments with inflation.
The current law governing Social Security payments is quite clear - when the Trust Funds run out, Social Security payments get slashed to only what can be covered by payroll taxes. The federal government actually has no legal obligation to make the payments shown in the Social Security tables, it only has to pay what it has the cash available to pay. Anyone who doubts that needs to go read some source documents, such as the Trustee's report for the Social Security Administration.
If the money isn't there, the full payments do not have to be paid. If the money isn't there, then there is no need to inflation index the payments, either. That is the law.
So, when we say that we know with certainty that those payments will be made in full and with full inflation indexing, something remarkable is happening - we are (effectively) assuming into existence a promise that does not yet exist, but can be absolutely relied upon to be made in the future, despite the party in question (the United States government), insisting that they don't owe the money. And the hypothetical (but certain) promise in question would be the largest financial promise in United States history.
When an expert says that they know with absolute certainty what the value of Social Security payments will be in 20 or 30 years, we need to think about just what a remarkable assertion that is. The Trust Funds are expected to run out somewhere between the late 2020s and mid 2030s. To buy into the model, one has to assume foreknowledge of exactly what changes will be made to the Federal law a decade or more from now, and that the funding will be radically changed but there will be no compromises or modifications that would impact payments or inflation indexing.
To have absolutely certain knowledge of the outcome of what is likely to be an intensely controversial political battle that will be waged many years in the future - is an extraordinary assumption. But it is mandatory. Because if we don't have certain knowledge, then we can't place all those very high values on cash that won't be received until someone is in their 70s and 80s.
We also need to carefully distinguish between certain knowledge and opinion. Now someone may believe that the rules governing Social Security are likely to change because of the political pressure to do so, and that for the same political reasons, payments will probably continue as they were. They may think it likely that inflation indexing will work in the way that is expected.
But the issue with words like "opinion, "probably" and "likely", is that uncertainty remains. If uncertainty remains, then we really should be discounting future cash flows for risk. As soon as we do that, then the one factor model collapses, it is back to a variant of the two factor model, we return to the diverging exponential series on top and bottom, and the cash flows in our 60s become more important relative to the cash flows in our 80s. That can then change our results.
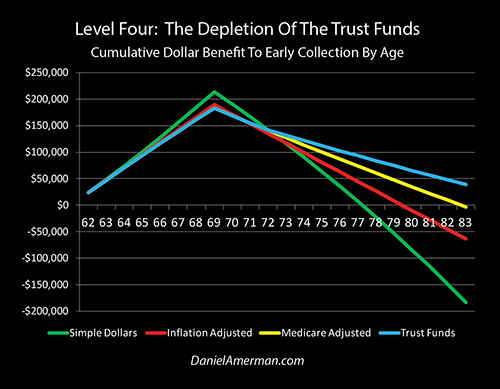
The four stage Social Security optimization analysis linked here does take into account such factors as Medicare premiums and Trust Fund depletion. As can be seen by comparing the four colored lines, as we expand the number of factors that we are taking into consideration, this can lead to substantial changes in the Social Security claiming decision process.
Using Personal Math To Make Better Decisions
When someone reaches the stage in life where they are making Social Security decisions, then they have had a lifetime to develop their own beliefs and opinions. Surely, when it comes time to make one of the most important financial decisions of their life - they have the right to choose their own assumptions based upon their own deeply held beliefs.
The moment that right to make a personal choice is accepted - then a necessary consequence is the collapse of the "one answer fits all" model. We no longer have one correct answer, that would be impossible. We no longer have financial education consisting of a group of experts choosing one set of theoretical assumptions, and saying this then is what all financially educated people should believe.
We now have myriad possible assumptions and combinations when it comes to Social Security payment reliability and inflation indexing. That also means that we potentially have myriad different potential "right answers" to the question of when to begin claiming Social Security benefits.
It would be easy to turn this into a debate about the correct rate of inflation or the future of Social Security for the nation as a whole, but that is completely unnecessary. This is all about you - not the attempt to force some sort of consensus, or to convince other people of your beliefs.
However, if we reject authoritative answers which are based on assumptions that we may fundamentally disagree with - then we still face the daunting question of evaluating more but smaller payments starting sooner, versus larger payments starting later. The choice may become one of the largest determinants of our personal standard of living for years - so how do we do a better job?
Fortunately, the bedrock future value and present value equations are very flexible tools, and can handle a wide variety of assumptions, as can more complex financial tools which are based upon them.
Do you believe that recent Social Security benefit increases averaging 0.75% per annum accurately reflect the rate of inflation that you have been experiencing in your own life? If not, and if you believe this situation is likely to persist, then your personal math needs to be based on partial inflation indexing, rather than the assumption of perfect inflation indexing.
In recent years an extraordinary mismatch has developed between theory and practice. We have tens of millions of people planning for retirement, who are being urged to make their decisions based upon the theory of perfect inflation indexing. Meanwhile, we have tens of millions of other people who are actually currently collecting Social Security while paying Medicare Part B premiums, and in practice they are finding out that their inflation indexing for net benefits has been almost non-existent.
Is that sort of mismatch important to you, or are you willing to overlook it if the experts are ignoring it? If that does matter to you, then your personal math should be taking Medicare premiums into account when making Social Security and other financial planning decisions - and the fundamental approach you take to making long term retirement decisions may have also just changed.
The United States government is heavily in debt, and it faces enormous financial pressures in the coming decades as a result of the Social Security and Medicare programs. Do you feel that you know with 100% certainty that Social Security benefits will be paid in full with full inflation indexing for the rest of your life - or do you think that there just might be even a chance that the future will work out differently?
If you think there is even a chance - then it could be a major mistake to make critical life decisions based upon a mathematical model which is based upon an assumption of complete certainty. If you think there is a risk that there will be a restructuring, or even just a long series of nicks and small cuts to the Social Security program over the years, then your personal math should include a risk component or some other form of adjustment. This means that your personal math will change the relative valuations of cash flows in your 60s and early 70s versus your late 70s and 80s - and this just might change your decision.
Some of those issues are explored in much more detail in the five part series linked here. These issues are critical, but they do not make our decision for us. We still have other important considerations such as taxes, employment, investments, spouses, family longevity, current health, and so forth.
Each of these can be determining factors that will help make that choice for us in terms of what is the best thing to do, whether it be collection of Social Security at age 62, or at 65 when we file for Medicare, or when we reach our Full Retirement Age (FRA), or at age 70, or at any of the other possible ages.
What using our personal math accomplishes is that it can give us better information - numbers that are consistent with what we truly believe - that we can then use in combination with the other considerations to find the best personal answer we can for what just may be one of the most important financial decisions that we will make.
This analysis is part of a series of related analyses, an overview of the rest of the series is linked here.
 What you have just read is an "eye-opener" financial analysis about critically important retirement decisions, and how they can change when we take a holistic look at the future.
What you have just read is an "eye-opener" financial analysis about critically important retirement decisions, and how they can change when we take a holistic look at the future.
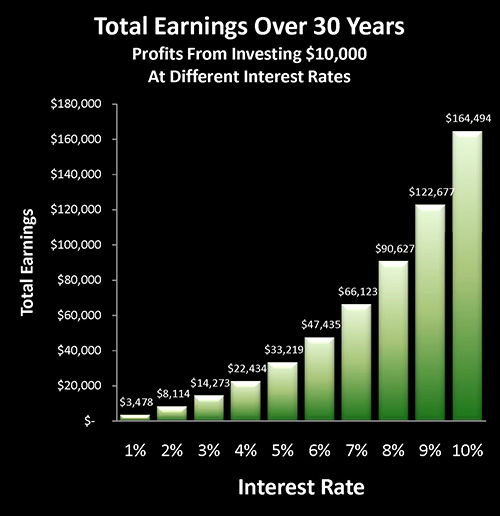
Retirement lifestyle is determined by both benefits and savings. Linked here is a related "eye-opener" that shows how the government's suppressing interest rates can reduce retirement investment wealth accumulation by 95% over thirty years, and how low interest rate policies are profoundly reducing standards of living for those already retired.
National debts have been reduced many times in many nations ─ and each time the lives of the citizens have changed. The "eye-opener" linked here reviews four traditional methods that can each change your daily life, and explores how governments use your personal savings to pay down their debts in a manner which is invisible to almost all voters.

The U.S. national debt is likely to change our daily lives in multiple ways over the coming decades, some of which are little understood by savers and investors. As shown in the first row of analyses in the matrix which is linked here, heavily indebted nations have major challenges when it comes to interest rates, inflation, financial stability and the ability to make Social Security and Medicare payments in full. As is examined in the second row of analyses, each of those national challenges can directly translate to life-changing personal challenges as well.






If you find these "eye-openers" to be interesting and useful, there is an entire free book of them available here, including many that are only in the book. The advantage to the book is that the tutorials can build on each other, so that in combination we can find ways of defending ourselves, and even learn how to position ourselves to benefit from the hidden redistributions of wealth.